公众号 数据精简DataSimp

　　数据精简DataSimp分享：信息与数据挖掘分析、数据科学研究前沿、数据资源现状和数据简化基础的学科知识、技术应用、产业科研、人物机构、新闻活动等信息。欢迎大家积极参与投稿，为数据科学产学研做贡献，使国人尽快提高人类信息管理能力，提高社会信息流通效率。本期内容：AlphaGo算法论文《精通围棋博弈的深层神经网络和树搜索算法》汉译（DeepMind围棋人工智能团队2016.1.28发表在《自然》杂志的nature16961原文翻译，人工智能之机器学习经典收藏版）、公号附录（大数据存储单位和数据简化DataSimp公众号简介）。

　　精通围棋博弈的深层神经网络和树搜索算法

　　作者：

　　①戴维·斯尔弗1*，②黄士杰1*，③克里斯·J。·麦迪逊1，④亚瑟·格斯1，⑤劳伦特·西弗瑞1，⑥乔治·范登·德里施1，⑦朱利安·施立特威泽1，⑧扬尼斯·安东诺娄1，⑨吠陀·潘聂施尔万1，⑩马克·兰多特1，⑪伞德·迪勒曼1，⑫多米尼克·格鲁1，⑬约翰·纳姆2，⑭纳尔 卡尔克布伦纳1，⑮伊利亚·萨茨基弗2，⑯蒂莫西·李烈克莱普1，⑰马德琳·里奇1，⑱科瑞·卡瓦口格鲁1，⑲托雷·格雷佩尔1，和⑳戴密斯·哈萨比斯1

　　作者单位说明：1谷歌DeepMind，英国伦敦EC4A 3TW，新街广场5号。2谷歌，美国加利福尼亚州94043，景山，剧场路1600号。*这些作者对这项工作作出了同等贡献。

　　中文翻译者说明*：

　　原文发表在《自然》2016年1月28日第529卷，484-489页，保留所有权利。©英国麦克米伦出版公司2016版权。本文汉语译者基于“忠于原文”原则全文翻译。同时参考自然杂志官网http://www.nature.com/nature/journal/v529/n7587/full/nature16961.html，由十五部分组成：摘要、导言、策略网络的监督学习、策略网络的强化学习、估值网络的强化学习、基于策略网络和估值网络的搜索算法、AlphaGo博弈算力评估、讨论、方法、参考文献、致谢、作者信息、扩展数据图像和表格、补充资料和网站评论。本文翻译到算力评估。网站提示：邮件可发至戴维·斯尔弗（davidsilver@google.com）或Demis Hassabis戴密斯·哈萨比斯（demishassabis @google.com）。

　　欢迎读者阅读原文，加强学习理解、掌握应用核心信息技术。时间仓促，疏漏之处难免，敬请提出宝贵意见。中文译者：秦陇纪-数据简化DataSimp（贡献3/5以上），姬向军-陕西师范大学，杨武霖-中国空间技术研究院，池绍杰-北京工业大学。（转载本公号文章请注明作者、出处、时间等信息，如“此文转自：数据简化DataSimp英译组秦陇纪等人；©微信公号：数据简化DataSimp；2016.3.15Tue译著©。”字样，详情邮件咨询QinDragon2010@qq.com，本文正在投稿，转载请保留本信息。欢迎数据科学和人工智能学界、产业界同仁赐稿。）

　　摘要：

　　由于海量搜索空间、评估棋局和落子行为的难度，围棋长期以来被视为人工智能领域最具挑战的经典游戏。这里，我们介绍一种新的电脑围棋算法：使用“价值网络”评估棋局、“策略网络”选择落子。这些深层神经网络，是由人类专家博弈训练的监督学习和电脑自我博弈训练的强化学习，共同构成的一种新型组合。没有任何预先搜索的情境下，这些神经网络能与顶尖水平的、模拟了千万次随机自我博弈的蒙特卡洛树搜索程序下围棋。我们还介绍一种新的搜索算法：结合了估值和策略网络的蒙特卡洛模拟算法。用这种搜索算法，我们的程序AlphaGo与其它围棋程序对弈达到99.8%的胜率，并以5比0击败了人类的欧洲围棋冠军。这是计算机程序第一次在标准围棋比赛中击败一个人类职业棋手——以前这被认为是需要至少十年以上才能实现的伟业。

　　导言：

　　完美信息类游戏都有一种最优值函数v*（s），从所有游戏者完美对弈时每一棋盘局面或状态s，判断出游戏结果。这类游戏可以通过递归计算一个约含bd种可能落子情况序列的搜索树，求得上述最优值函数来解决。这里，b是游戏广度（每个局面可合法落子的数量），d是游戏深度（对弈步数）。在国际象棋（b≈35，d≈80）1，特别是围棋（b≈250，d≈150）1等大型游戏中，虽然穷举搜索并不可取2，3，但有两种常规方法可以减少其有效搜索空间。第一种方法，搜索深度可以通过局面评估来降低：用状态s截断搜索树，将s的下级子树用预测状态s结果的近似值函数v（s）≈v*（s）代替。这种做法在国际象棋4，跳棋5和奥赛罗6中取得了超过人类的性能；但由于围棋7的复杂性，这种做法据信在围棋中变得棘手。第二种方法，搜索广度可以用局面s中表示可能落子a的策略函数p（a|s）产生的概率分布的弈法抽样来降低。例如，蒙特卡洛走子算法8搜索到最大深度时无任何分支，而是用策略变量p为对弈双方的长弈法序列采样。大体上，这些走子行为提供了一种有效的局面评估，在五子棋8、拼字游戏9和低水平业余围棋比赛10中均实现了超越人类水平的性能。

　　蒙特卡洛树搜索（MCTS）11，12用蒙特卡洛走子来估算一个搜索树中每个状态的值。随着更多模拟情况的执行，该搜索树生长变大、相关值变得更加准确。随着时间的推移，通过选择那些较高估值的子树，搜索过程中选择弈法的策略也得到了提高。该策略渐进收敛于最优弈法，对应的估值结果收敛于该最优值函数12。当下最强的围棋程序都基于MCTS，通过预测人类高手落子情况而训练的一些策略，来增强性能13。这些策略大都把此搜索过程限制在高概率弈法，以及走子时的弈法采样。该方法已经在很强的业余博弈中取得了成功13–15。然而，以前的做法仅限于浅层策略13–15，或某些基于一种带输入型特征值的线性函数组合的估值函数。

　　近来，深度卷积神经网络在视觉领域达到前所未有的高性能：例如图像分类17、人脸识别18、雅达利游戏19。他们用重叠排列的多层神经元，逐步构建图像的局部抽象表征20。我们在围棋中采用类似架构：通过把棋局看做为一个19×19的图像，使用若干卷积层构造该局面的表征值。用这些神经网络，我们来减少有效深度及搜索树广度：用一个估值网络评估棋局，用一个策略网络做弈法取样。

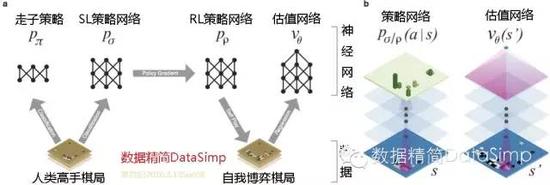
　　我们用一种由机器学习若干阶段组成的管道来训练这些神经网络（图1）。开始阶段，我们直接使用人类高手的落子弈法训练一种有监督学习（SL）型走棋策略网络pσ。此阶段提供快速、高效的带有即时反馈和高品质梯度的机器学习更新数据。类似以前的做法13，15，我们也训练了一个快速走棋策略pπ，能对走子时的弈法快速采样。接下来的阶段，我们训练一种强化学习（RL）型的走棋策略网络pρ，通过优化那些自我博弈的最终结果，来提高前面的SL策略网络。此阶段是将该策略调校到赢取比赛的正确目标上，而非最大程度的预测准确性。最后阶段，我们训练一种估值网络Vθ，来预测那些采用RL走棋策略网络自我博弈的赢家。我们的程序AlphaGo，用MCTS有效结合了策略和估值网络。

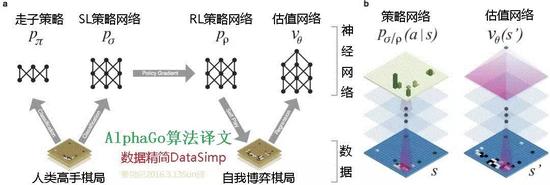
　　图1：神经网络训练管道和架构

　　左边图1a，一种快速走子策略pπ和监督学习（SL）策略网络pσ被训练，用来预测一个局面数据集中人类高手的落子情况。一种强化学习（RL）策略网络pρ按该SL策略网络进行初始化，然后对前一版策略网络用策略梯度学习来最大化该结果（即赢得更多的比赛）。通过和这个RL策略网络自我博弈，产生一个新数据集。最后，一种估值网络vθ由回归训练的，用来预测此自我博弈数据集里面局面的预期结果（即是否当前玩家获胜）。右边图1b，AlphaGo神经网络架构的示意图。图中的策略网络表示：作为输入变量的棋局s，通过带参数σ（SL策略网络）或ρ（RL策略网络）的许多卷积层，输出合法落子情况a的概率分布或，由此局面概率图来呈现。此估值网络同样使用许多带参数θ的卷积层，但输出一个用来预测局面sʹ预期结果的标量值vθ（sʹ）。

　　1、策略网络的监督学习

　　训练管道第一阶段，我们按以前的做法用监督学习预测围棋中高手的落子情况13，21–24。此SL策略网络pσ（a|s）在带有权重数组变量σ和整流器非线性特征值数组的卷积层间交替使用。最终的softmax层输出一个所有合法落子情况的概率分布a。此策略网络的输入变量s是一个棋局状态的简单标识变量（见扩展数据表2）。策略网络基于随机采样的棋盘情形-操作对（s，a）做训练：采用随机梯度升序法，在选定状态s时，取人类落子a的最大相似度，

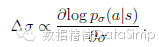
　　我们用KGS围棋服务器上的3000万种棋局，训练了一个13层策略网络，称之为SL策略网络。对比其他研究团体提交的44.4%顶尖水准，该网络在一个公开测试数据集上预测高手落子情况：采用全部输入型特征值可达57.0%精度，只采用原始棋局和落子历史数据做为输入可达55.7%（全部结果在扩展数据表3）24。准确性上小的改进，可导致算力大幅提高（图2a）；较大网络亦可实现更好的精度，但在搜索过程中的评价会变慢。我们也训练了一个快速、但低准确度的走子策略pπ（a|s），采用一种带权重π的小图式特征量的线性softmax层（参见扩展数据表4），这样，仅用2微秒选择一种弈法可以达到24.2%的精确度，而不是此策略网络的3毫秒。

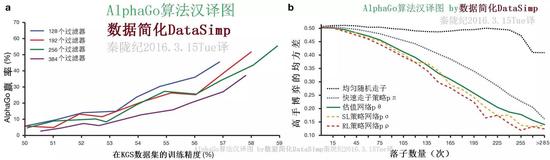
　　图2：策略和估值网络的算力和准确性。

　　图2a，标尺图展示作为一个他们训练精确性函数的策略网络博弈算力。每个卷积层分别有128，192，256和384个过滤器的策略网络在训练期间被定期评估；此图显示AlphaGo运用那种策略网络与比赛版AlphaGo对战的胜率。图2b，该估值网络和不同策略走子弈法之间的估值精度比较。从人类专家博弈中做局面和结果采样。每局都由一个单一向前传递的估值网络vθ，或100步走子情况的平均结果做评估，用均匀随机走子，快速走子策略pπ，SL策略网络pσ或RL策略网络pρ等使局面充分被评估。此预测值和实际博弈间的均方差，绘制在博弈阶段（多少落子已经在给定局面）。

　　2、策略网络的增强学习

　　训练管道第二阶段，旨在用策略梯度型增强学习（RL）来提高之前的策略网络25，26。这种RL策略网络pρ在结构上与SL策略网络相同，其权重ρ被初始化为相同值：ρ=σ。我们使其在当前策略网络pρ和某个随机选择的上次迭代产生的策略网络之间进行对弈。这种方法的训练，要用随机化的存有对手稳定态的数据池，来防止对当前策略的过度拟合。我们使用报酬函数r（s），对所有非终端时间步长t<T时，赋值为0。其结果值zt = ± r（sT）是博弈结束时的终端奖励：按照当前博弈者在时间步长t时的预期，给胜方+1、败方−1。权重在每一次步长变量t时，按照预期结果最大值的方向，进行随机梯度升序更新25。

　　博弈中我们评估该RL策略网络的性能，从弈法输出概率分布对每一次落子采样为。与SL策略网络正面博弈时，RL策略网络赢得了80%以上。我们还用最厉害的开源围棋程序Pachi14来测试。那是一种复杂的蒙特卡洛搜索程序——KGS服务器上排名第二的业余选手dan，每个落子要执行10万次模拟。不用任何搜索，RL策略网络赢得了85%与Pachi的对弈。对照以前的顶尖水平，仅基于卷积网络的监督学习与Pachi23对弈只能赢得11%、与较弱程序Fuego24对弈为12%。

　　3、估值网络的增强学习

　　最后阶段的训练管道聚焦在对棋局的评估，用一个估值函数vp（s）做估计，给棋局s中两个使用策略p的博弈者预测结果28，29，30。

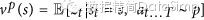
　　理想情况下，我们想知道完美博弈v*（s）中的该最优值函数；实践中，我们用值函数代替做估算，作为最强策略用在RL策略网络pρ。我们用带权重数组θ的估值网络vθ（s）对此估值函数做近似，

　　。该神经网络具有一种与此估值函数相似的结构，但输出一个单一预测，而不是一个概率分布。我们用状态-结果对（s， z）回归，训练该估值网络权重，使用随机梯度降序来最小化该预测值vθ（s）和相应结果z间的均方差（MSE），

　　用包含全部博弈的数据集，来预测对弈结果的幼稚做法，会导致过度拟合。其错误在于：连续棋局是紧密相关的，不同处只有一枚棋子，但其回归目标被该完整对弈所共用。我们用这种方法在KGS数据集做过训练，该估值网络记住了那些博弈结果，并没有推广到新棋局，相比此训练集上的0.19，此测试集上达到了0.37的最小均方差（MSE）。为了缓解这个问题，我们生成了一个新的含有3000万明显不同棋局的自我博弈数据集，其每个采样都来自于某一单独对弈。每一场对弈都是在上述RL策略网络与自身之间进行，直到博弈结束。在该数据集上的训练，采用训练和测试数据集分别可达到0.226和0.234的均方差，这表明最小的过拟合。图2b显示了上述估值网络的棋局评估精度，相比使用快速走子策略pπ的蒙特卡洛走子程序，此估值函数一贯都是更加准确。一种vθ（s）单一评价函数也接近使用RL策略网络Pρ的蒙特卡洛程序的精度，且使用少于15000次的计算量。

　　4。基于策略网络和估值网络的搜索算法

　　AlphaGo在一种采用前向搜索选择弈法的MCTS算法里，结合使用策略和估值网络（图3）。每个搜索树边界（s， a）存储：弈法值Q（s， a），访问计数N（s， a），和前驱概率P（s， a）。从当前根状态出发，该搜索树用模拟（指已完成的博弈中做无备份降序）做遍历。在每次模拟的每个时间步长t，从状态st内选出一个弈法at，

　　当满足，最大弈法值加上与前驱概率成正比、但与访问计数成反比的奖励值：

　　，能有效促进对搜索空间的探索。当这个遍历在步骤L，搜索一个叶节点sL时，该叶节点可能被展开。该叶节点的局面sL仅通过SL型策略网络pσ处理一次。该输出概率被存储为每次合法弈法a的前驱概率。

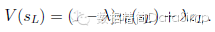
　　这个叶节点通过两种不同方式被评估：一种是通过估值网络vθ（sL）；第二种是，通过一种随机落子的结果值zL，直到使用快速走子策略pπ在步长T时结束博弈。这些评价被组合起来，用一种混合参数λ，进入一个叶节点估值V（sL）：

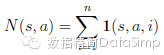
　　模拟结束时，遍历过的所有边界其弈法值和和访问计数就会被更新。每个边界累加其访问计数值，和所有经过该边界做的模拟的平均估值：

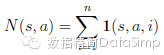
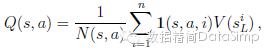
　　式中是其第i次模拟的叶节点，1（s， a， i）代表第i次模拟中一个边界（s， a）是否被访问。当该搜索结束时，本算法选择这次初始局面模拟的访问计数最多的弈法来落子。

　　图3：AlphaGo的蒙特卡洛树搜索。

　　图3a，每次模拟都遍历带最大弈法值Q的那个边界节点，与一个由那个边界节点存储的前驱概率产生的奖励值u（P）相加。图3b，此叶节点可能被展开；新节点采用策略网络pσ，其输出概率值P被存储在每个弈法的前驱概率P中。图3c，模拟结束后，此叶节点被两种方法评估：采用估值网络vθ；和博弈最后用快速落子策略pπ进运行一次走子，然后用函数r计算此赢家的估值。图3d，弈法值Q被更新，用来追踪所有估值r（·）的中间值和那个弈法下面的子树vθ（·）。

　　值得注意的是，此AlphaGo的SL策略网络pσ比那个加强型RL策略网络pρ表现地更好，主要原因在于人类选择最有前景落子中一种可变化的弈法，而RL仅对该单次落子做最优化。然而，从强化后的RL策略网络中推导的估值函数，在AlphaGo的性能要优于SL策略网络推导出的估值函数。

　　跟传统启发式搜索相比，策略和估值网络需要高出几个数量级的计算量。为了有效结合MCTS和深度神经网络，AlphaGo采用异步多线程搜索，在多CPU上执行模拟、多GPU并行计算策略和估值网络。本最终版AlphaGo使用了40个搜索线程、48个CPU和8个GPU。我们也应用了一种分布式AlphaGo版本，部署在多台机器上、40个搜索线程、1202个CPU和176个GPU。方法章节提供异步和分布式MCTS全部细节。

　　5.AlphaGo博弈算力评估

　　为了评估AlphaGo，我们在几个版本的AlphaGo和其它几种围棋程序之间运行了一场内部竞赛，包括最强商业软件Crazy Stone13，和Zen，和最强开源程序Pachi14和Fuego15。所有这些程序基于高性能MCTS算法。此外，我们纳入了开源程序GnuGo，一种使用优于MCTS的顶级水平搜索算法的围棋程序。在比赛中，所有软件每一步都只有5s中的计算时间。

　　（未完待续。感谢翻译过程中Dr何万青Dr余凯ETS颜为民等人的译文建议。欢迎大家关注译文质量，我们共同提高。）

　　附录一、大数据存储单位（TB以上）

　　计算机存储最小的基本单位是bit，按顺序给出所有计量单位：bit位（无法分割）、Byte字节（10^0）、KB千字节（10^1）、MB兆字节（10^3）、GB吉字节（10^6）、TB太字节（10^9）、PB拍字节（10^12）、EB艾字节（10^15）、ZB泽字节（10^18）、YB尧字节（10^21）、BB（10^24）、NB（10^27）、DB（10^30）。大数据存储单位大都TB以上，按照进率1024（2的十次方）来计算：

　　1 TB = 1，024 GB（Gigabyte吉字节） = 1，048，576 MB（Megabytes兆字节）；

　　1 PB（Petabyte千万亿字节，拍字节） = 1，024 TB（Terabytes） = 1，048，576 GB；

　　1 EB（Exabyte百亿亿字节，艾字节） = 1，024 PB（Petabytes） = 1，048，576 TB；

　　1 ZB（Zettabyte十万亿亿字节，泽字节） = 1，024 EB（Exabytes） = 1，048，576 PB；

　　1 YB（Yottabyte一亿亿亿字节，尧字节） = 1，024 ZB（Zettabytes） = 1，048，576 EB；

　　1 BB（Brontobyte一千亿亿亿字节） = 1，024 YB（Yottabytes） = 1，048，576 ZB；

　　1 NB（N？Geopbyte？没查到翻译） = 1，024 BB（Brontobytes） = 1，048，576 YB；

　　1 DB（？没查到） = 1，024 NB = 1，048，576 BB。

　　注：进制单位全称及译音 yotta [尧]它 Y。 10^21， zetta [泽]它 Z。 10^18， exa [艾]可萨 E。 10^15， peta [拍]它 P。 10^12， tera [太]拉 T。 10^9， giga [吉]咖 G。 10^6， mega [兆] M。 10^3“兆”为百万级数量单位。（秦陇纪16科普版）